Binary Tree Introduction and Important Traversals
Introduction to Trees | Types of Trees
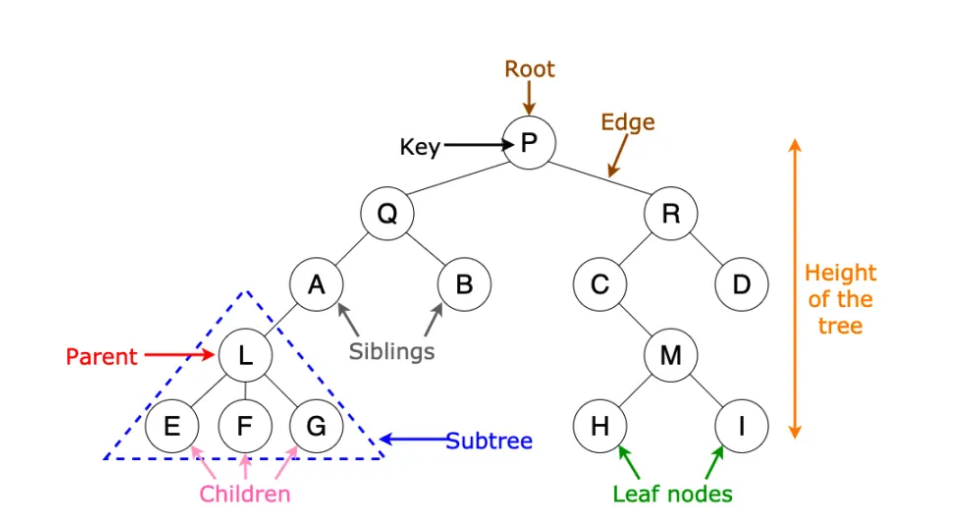
Binary Tree Introduction
- A node can have only two children → Binary Tree
-
A full binary tree is a tree where every node has 0 or 2 children.
- Complete Binary Tree:
- All levels are completely filled except the last level.
- The last level has all nodes as left as possible.
- Perfect Binary Tree: All leaf nodes are at the same level.
- Balanced Binary Tree: Height at maximum of log(N) where N is the number of nodes.
- Degenerate Binary Tree: Essentially a linked list.
Binary Tree Representation in C++
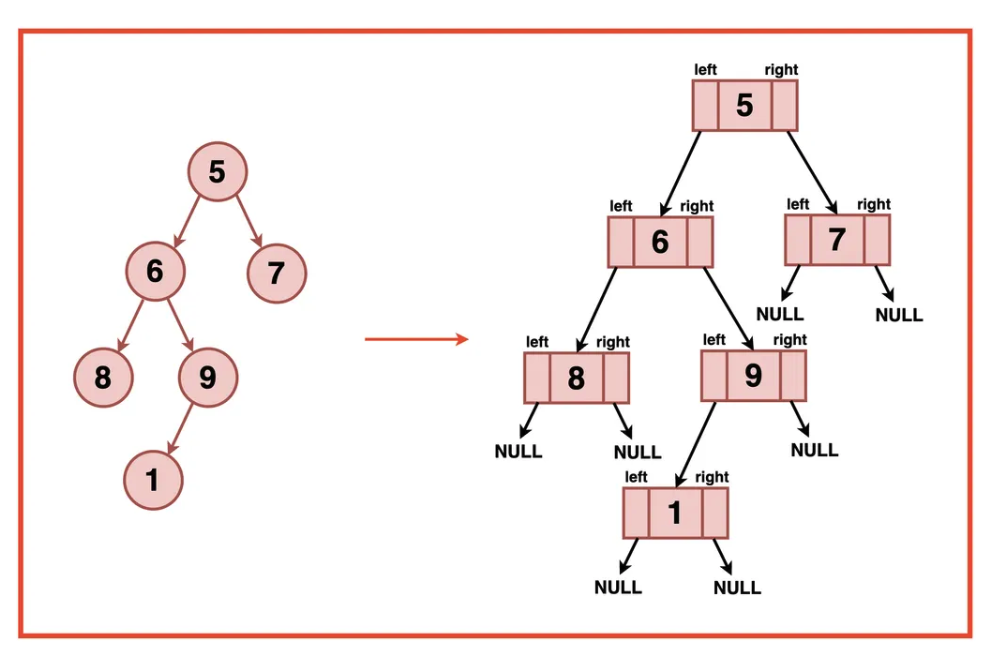
Tree Representation in C++
Binary tree can be represented in code as follows:
struct Node{
int data;
struct Node* left;
struct Node* right;
Node(int val){
data = val;
left = right = NULL;
}
}
Initializing it in main function looks as follows:
int main(){
struct Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->right = new Node(5)
}
Traversal Techniques
- BFS
- Level order traversal
- DFS
- Inorder traversal (left root right)
- Preorder traversal (root left right)
- Postorder traversal (left right root)
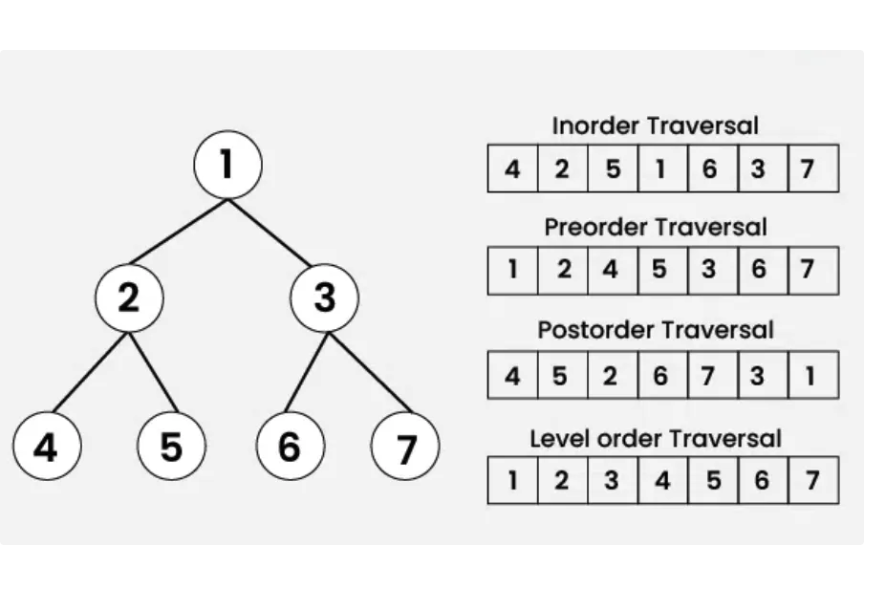
Types of Traversals
Go the subtree of each node and apply the same order to get the traversal for the whole tree
Preorder Traversal
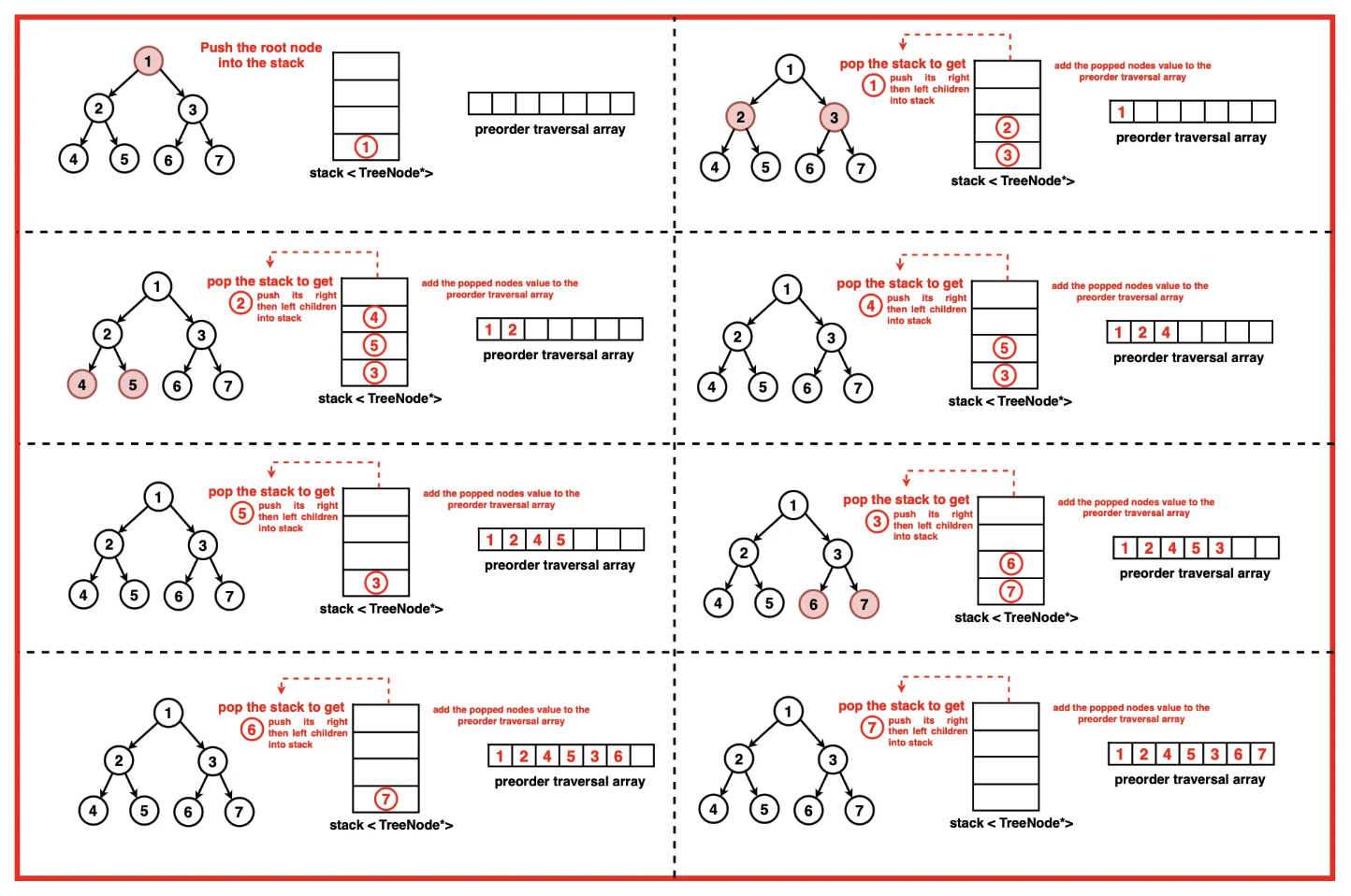
Preorder Traversal
Implementation of preorder traversal in C++
void preorder(node){
if(node == NULL) return;
cout << node->data << endl;
preorder(node->left);
preorder(node->right);
}
Time complexity: O(N), Space complexity: O(N)
Iterative Preorder traversal in C++ [1 stack required]
- Push the root of the tree into the stack.
- Now, while the stack is non empty,
- pop the node at the top of the stack, call it curr_node
- in a while loop
- print the curr_node
- for each node encountered, push its right child to the top of the stack
- keep visiting all the left children of the curr_node (make curr_node equal to its left child)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
if(root == NULL) return res;
stack<TreeNode*> stack;
stack.push(root);
while(!stack.empty()){
TreeNode* curr_node = stack.top();
stack.pop();
TreeNode* popped_node = curr_node;
while(curr_node != NULL){
res.push_back(curr_node->val);
if(curr_node->right != NULL) stack.push(curr_node->right);
curr_node = curr_node->left;
}
}
return res;
}
};
Inorder Traversal
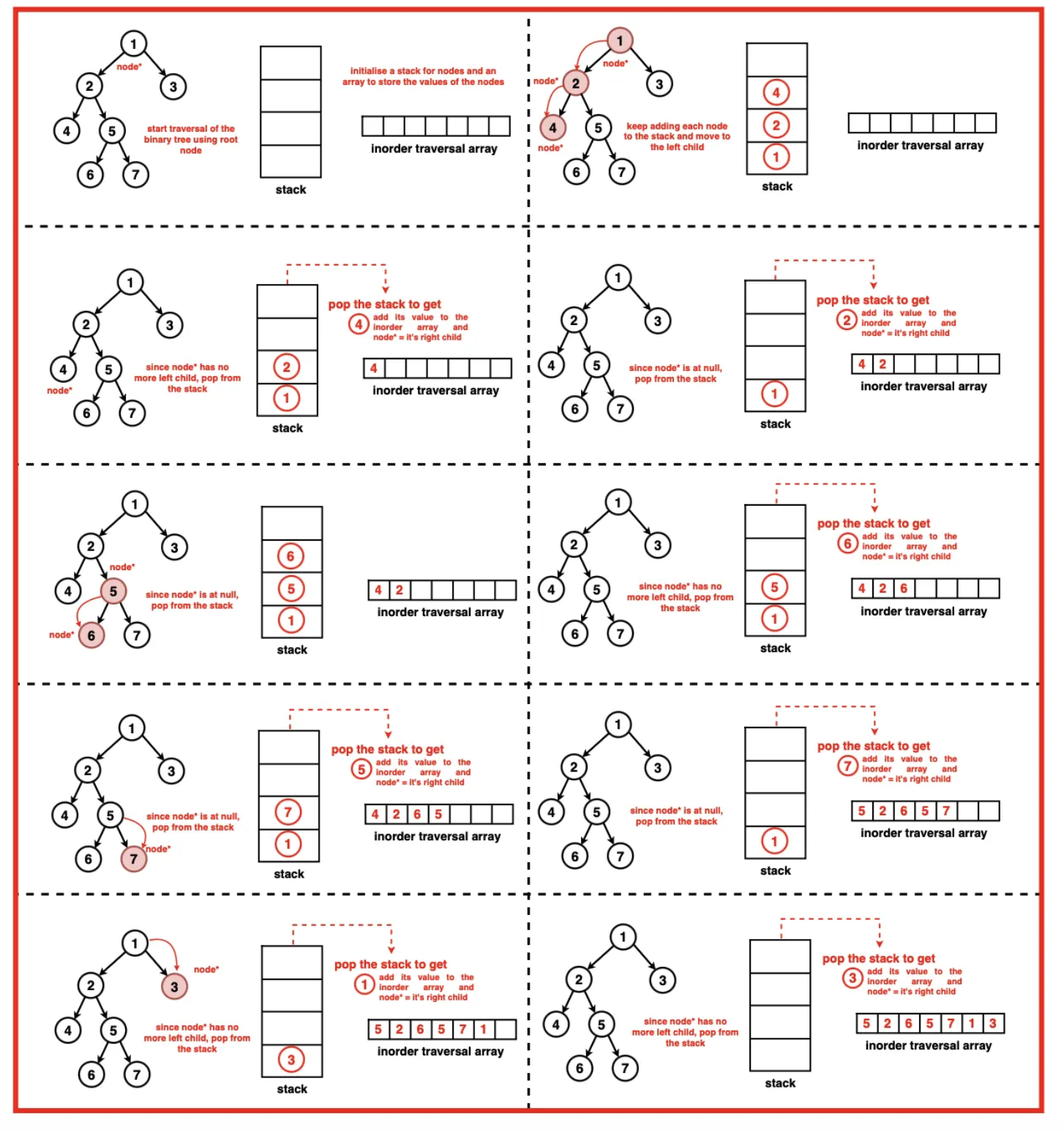
Inorder Traversal
Implementation of Inorder traversal in C++
void inorder(node){
if(node == NULL) return;
inorder(node->left);
cout << node->data << endl;
inorder(node->right);
}
Time complexity: O(N), Space complexity: O(N)
Iterative Inorder Traversal in C++ [1 Stack]
- Mark the curr_node as root
- While the curr_node is not empty
- Keep pushing the curr_node to the stack
- Change curr_node to curr_node→left
- While the stack is not empty
- Get the top element and mark it as curr_node
- Pop it and add it to the result or print it
- If the right child is not null,
- Add the right child and mark it as node t
- While t is not null
- Keep adding the left child of t
- t is changed to t→left
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
if(root == NULL) return res;
stack<TreeNode*> stack;
TreeNode* curr_node = root;
while(curr_node != NULL){
stack.push(curr_node);
curr_node = curr_node->left;
}
while(!stack.empty()){
TreeNode* curr_node = stack.top();
stack.pop();
res.push_back(curr_node->val);
if(curr_node->right != NULL) {
TreeNode* t = curr_node->right;
while(t != NULL){
stack.push(t);
t = t->left;
}
}
}
return res;
}
};
Postorder Traversal
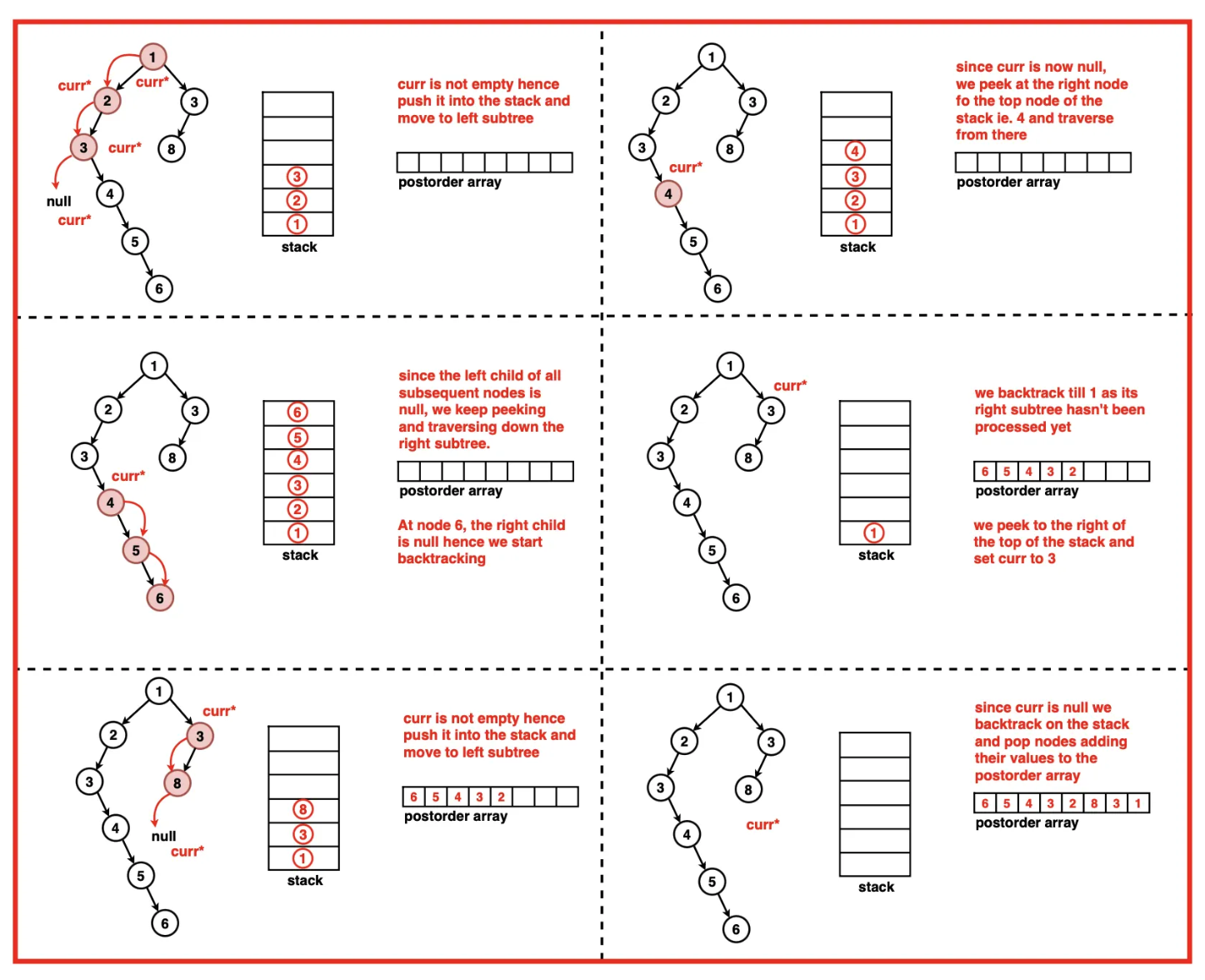
Postorder Traversal
Implementation of postorder traversal in C++
void postorder(node){
if(node == NULL) return;
postorder(node->left);
postorder(node->right);
cout << node->data << endl;
}
Time complexity: O(N), Space complexity: O(N)
Iterative Postorder traversal in C++ [2 stacks required]
- Maintain two stacks: st1, st2
- Add the root node to st1
- Now, while the st1 is not empty, do the following
- Get the top node of st1
- pop it
- push the popped node to the top of st2
- push the left child of popped node to the top of st1
- push the right child of popped node to the top of st1
- While the st2 is not empty
- pop the top element
- Stack 2 printing will give us the final post order traversal.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
if(root == NULL) return res;
stack<TreeNode*> st1, st2;
st1.push(root);
while(!st1.empty()){
TreeNode* curr_node = st1.top();
st1.pop();
st2.push(curr_node);
if(curr_node->left != NULL){
st1.push(curr_node->left);
}
if(curr_node->right != NULL){
st1.push(curr_node->right);
}
}
while(!st2.empty()){
res.push_back(st2.top()->val);
st2.pop();
}
return res;
}
};
Level Order Traversal
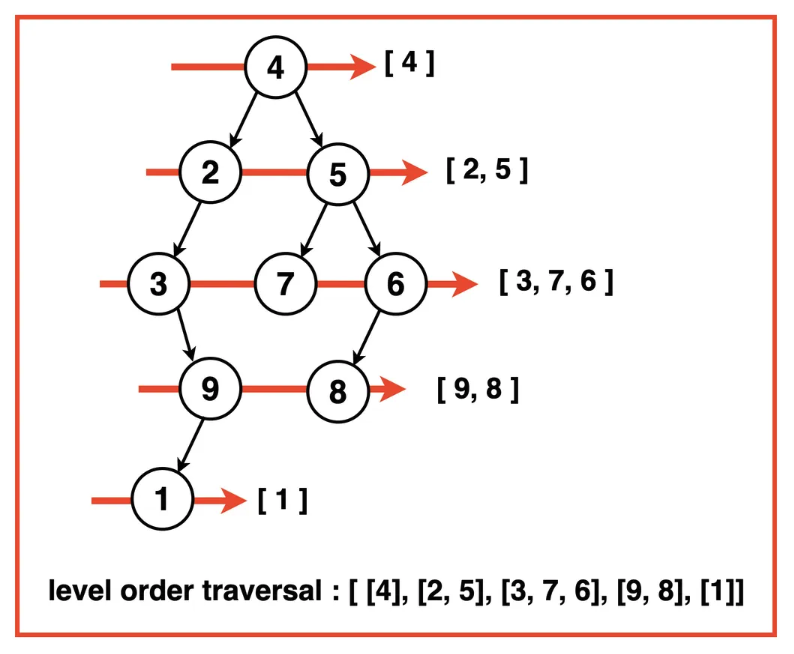
Level Order Traversal (Breadth First)
Implementation of level traversal in C++
- Simple BFS pattern.
- IMPORTANT: You need to maintain a variable queue_size that “snapshots” current queue size before processing each level’s elements.
// Level Order Traversal in C++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
if(root == NULL) return res;
queue<TreeNode*> q;
q.push(root);
int level = 1;
while(!q.empty()){
vector<int> curr_level;
int curr_q_size = q.size();
for(int i = 0; i < curr_q_size; i++){
TreeNode* curr_node = q.front();
curr_level.push_back(curr_node->val);
q.pop();
for(TreeNode* n: {curr_node->left, curr_node->right}){
if(n != NULL) q.push(n);
}
level++;
}
res.push_back(curr_level);
}
return res;
}
};
Zigzag Level Order Traversal
- There is a way to follow the BFS pattern for Level order traversal, and just use a built-in function to reverse each level before adding it to the final result.
- We can skip the reversing if we can maintain a position variable that specifies from which position we should start filling up each level’s elements.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> res;
if(root == NULL) return res;
queue<TreeNode*> q;
q.push(root);
bool to_reverse = false;
while(!q.empty()){
int q_size = q.size();
vector<int> curr_level(q_size);
for(int i = 0; i < q_size; i++){
TreeNode* curr_node = q.front();
int pos = (to_reverse) ? q_size - 1 - i : i;
curr_level[pos] = curr_node->val;
q.pop();
for(TreeNode* n: {curr_node->left, curr_node->right}){
if( n!= NULL) q.push(n);
}
}
res.push_back(curr_level);
to_reverse = !to_reverse;
}
return res;
}
};
Enjoy Reading This Article?
Here are some more articles you might like to read next: