Tree traversals in O(1) space? Let's do Morris Traversals

Can We Traverse a Tree Without Extra Space?

Picture this: You’re standing at the foot of a massive tree (pun intended), trying to navigate its branches. Normally, you’d need a notebook (a call stack for recursion) or a basket (a stack data structure) to keep track of where you’ve been. But what if you had no storage at all? Could you still navigate the tree?

That’s exactly what Morris Traversal does. It lets us traverse a binary tree without using recursion or an explicit stack—just by cleverly reusing the tree structure itself. And the best part? It works in O(1) space!

The Secret: Threading the Tree

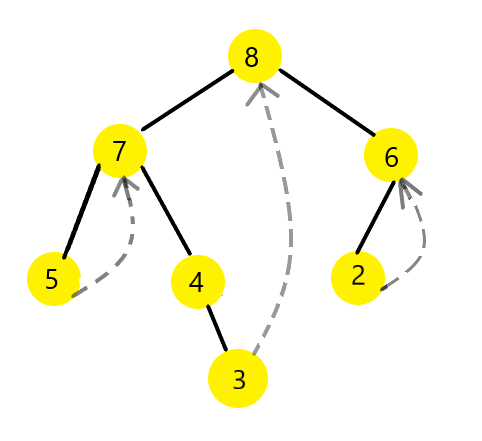
Normally, when we do an inorder traversal (Left → Root → Right), we use recursion or a stack to remember our path. But Morris Traversal takes a different approach—it modifies the tree temporarily by creating threaded links. These links act as breadcrumbs, guiding us back when needed. Here’s how it works:

Algorithm Breakdown

1. Start at the root (curr).
2. If curr has no left child, print curr (process the node) and move to curr->right.
3. If curr has a left child:
   • Find its inorder predecessor (the rightmost node in curr->left subtree).
   • If the predecessor’s right is NULL:
     • Make it point to curr (this is our breadcrumb).
     • Move curr to its left.
   • If the predecessor’s right is already pointing to curr (breadcrumb exists):
     • Remove the thread (restore the tree).
     • Print curr.
     • Move curr to its right child.

By following this method, every node is visited exactly twice, ensuring an efficient traversal.

Show Me the Code

Here’s the C++ implementation of Morris Inorder Traversal:

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode* curr = root;

        while (curr != NULL) {
            if (curr->left == NULL) {
                res.push_back(curr->val);
                curr = curr->right;
            } else {
                TreeNode* prev = curr->left;
                while (prev->right && prev->right != curr) {
                    prev = prev->right;
                }
                
                if (prev->right == NULL) {
                    prev->right = curr;
                    curr = curr->left;
                } else {
                    prev->right = NULL;
                    res.push_back(curr->val);
                    curr = curr->right;
                }
            }
        }
        return res;
    }
};

Why Is This Efficient?

• Time Complexity: O(n) → Each node is visited at most twice (once when threading, once when removing the thread).
• Space Complexity: O(1) → No extra memory apart from a few pointers.

When Should You Use Morris Traversal?

This trick is particularly useful when:

✅ You need to traverse a tree but don’t want extra space overhead (e.g., limited memory environments).

✅ You don’t mind temporarily modifying the tree (Morris Traversal restores it after use).

✅ You need an efficient way to do inorder traversal without recursion or an explicit stack.

But Wait—What About Preorder?

Yes! You can adapt Morris Traversal for preorder traversal as well. The only difference is that you process the node before moving left instead of after restoring the thread.

Morris Preorder Traversal (C++)

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode* curr = root;

        while (curr != NULL) {
            if (curr->left == NULL) {
                res.push_back(curr->val);
                curr = curr->right;
            } else {
                TreeNode* prev = curr->left;
                while (prev->right && prev->right != curr) {
                    prev = prev->right;
                }
                
                if (prev->right == NULL) {
                    res.push_back(curr->val);
                    prev->right = curr;
                    curr = curr->left;
                } else {
                    prev->right = NULL;
                    curr = curr->right;
                }
            }
        }
        return res;
    }
};

Final Thoughts

Morris Traversal is one of those mind-bending techniques that feel almost magical the first time you see them. It challenges the way we normally think about traversing trees, proving that sometimes, the best solutions come from rethinking the problem entirely.

So the next time someone says O(1) space tree traversal is impossible, just smile and say, “Ever heard of Morris Traversal?” 😉!